Мифы про массу автомобиля

Итак, самые распространенные мифы в части физики происходящего относятся к массе автомобиля (или его весу, не суть важно, не будем буквоедствовать). Поэтому, стоит детально разобраться, что к чему.
Миф №1. Тяжелый автомобиль медленнее поворачивает
Люди, плохо помнящие школьный курс физики, мотивирует это тем, что инерция (сила), которая тащит автомобиль наружу поворота, прямо пропорциональна массе автомобиля.
Давайте разбираться по порядку:
- В инерциальной системе отсчета (коей можно считать Землю, если мы рассматриваем происходящее на ней) силы инерции не существует в принципе. Наоборот, чтобы заставить автомобиль поворачивать, нужно приложить к нему силу, направленную к центру поворота. В противном случае, автомобиль будет двигаться прямолинейно и равномерно, если на него не действуют силы (или их равнодействующая равна 0), что строго соответствует I закону Ньютона. С этим разобрались, едем дальше.
- Чтобы заставить автомобиль поворачивать (описывать дугу), нам необходимо придать ему ускорение. Из физики мы знаем, что это ускорение a, называемое центростремительным, равно
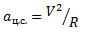 где V — скорость автомобиля, R — радиус поворота.
где V — скорость автомобиля, R — радиус поворота. - Т.е. нам нужно придать автомобилю силу F, равную
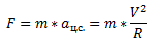 где m — масса автомобиля.
где m — масса автомобиля. - Теперь нам нужно понять, откуда эта сила берется. Когда мы поворачиваем руль, покрышки отталкиваются от дорожного полотна, тем самым создавая необходимую нам силу. Т.е. нужная нам сила — это горизонтальная составляющая силы реакции опоры (вертикальная N, обычно называемая весом авто, нас в данный момент не интересует). Называется такая сила — силой трения. Как нам известно из физики, сила трения Fтр (покоя или скольжения пока не важно) равна:
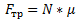 где N — та самая вертикальная составляющая или вес авто, а μ — коэффициент трения.
где N — та самая вертикальная составляющая или вес авто, а μ — коэффициент трения. - Если мы рассмотрим упрощенную модель — не будем рассматривать распределение веса автомобиля по каждому колесу, а возьмем автомобиль целиком, то мы прекрасно знаем, чему равна сила N, это, конечно же, N=m*g, где m — вновь масса авто, а g — ускорение свободного падения. Всевозможные аэродинамические силы мы сейчас не рассматриваем.
- Естественно, искомая сила F и сила трения Fтр в нашем случае должны быть равны, посему приравниваем два выражения и получаем уравнение:
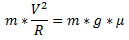 из которого прекрасно видно, что масса сокращается (т.к. находится по обе стороны уравнения).
из которого прекрасно видно, что масса сокращается (т.к. находится по обе стороны уравнения). - Т.к. результатом наших изысканий должна стать скорость прохождения поворота V, ее мы и выразим из этого уравнения (особо подозрительные могут проверить размерность уравнения):
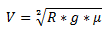
Итак, мы получили, что искомая скорость зависит от радиуса поворота R, ускорения свободного падения g и коэффициента трения μ. И не зависит от массы автомобиля m.
Эти же выкладки, естественно, подтверждает и практика. Никакой прямой зависимости скорости в повороте от массы не существует. Иначе бы автомобиль массой в тонну всегда в 2 раза быстрее проходил поворот, чем автомобиль массой в 2 тонны на той же резине. Такого в принципе не может быть! Поверь мне, выкладки, изложенные выше, многократно проверены многими участниками соревнований при помощи беспристрастной телеметрии. Ты и сам можешь это проверить, например, посадив себе пассажира и заправив полный бак.
Внимательные люди, хорошо знакомые с физикой, заподозрят меня в неточности. Действительно, тут я должен оговориться:
- Я сознательно выбрал упрощенную систему распределения веса автомобиля в повороте. В действительности наружное колесо нагружается сильнее, а внутреннее слабее, передние сильнее, задние обычно слабее. В целом, это не имеет никакого значения, т.к. у более тяжелого автомобиля это происходит ровно так же. Но есть нюанс в плане максимальной нагрузки на колесо, о чем в следующем пункте.
- Главное упрощение в выкладках выше касается пресловутого коэффициента сцепления μ. Проблема в том, что этот коэффициент (бывает покоя и скольжения) не постоянен в зависимости от вертикальной нагрузки. Это уже особенность поведения шины в реальной жизни. Скажу более простым языком, если на машину поставить, например, слишком узкую шину, то в какой-то момент, сколько ее не нагружай, сила трения расти не будет (или будет незначительно). Условно говоря, у шины есть диапазон нагрузок, внутри которого максимальный коэффициент трения остается практически постоянным. При выходе из этого диапазона максимальный коэффициент трения начинает падать. Я постараюсь подробно рассмотреть эту тему в отдельной статье, но пока будем основываться на этих упрощенных данных.
Проще говоря, если автомобилю подобрана резина с шириной, адекватной массе авто, то с максимальным коэффициентом трения будет все ок, он будет соответствовать таковому для всех покрышек этой модели.
Миф №2. Тяжелый автомобиль хуже тормозит
Забегая вперед, скажу, что здесь ровно тот же принцип и абсолютно аналогичные выводы, что и с предыдущим пунктом. С увеличением массы растет не только сила, требуемая для остановки автомобиля, но и сила трения. В уравнении также просто сокращается масса. Но для особо пытливых умов я разберу все по порядку:
- Для простоты представим себе, что оба автомобиля подлетают к повороту на одинаковой скорости и начинают тормозить с одного и того же места до полной остановки. Нам нужно вычислить тормозной путь. Опять же для простоты будем считать, что замедление происходит с постоянным ускорением (или перегрузкой), что при качественном торможении недалеко от истины. В таком случае тормозной путь будет равен:
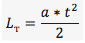
где a — ускорение замедления, а t — время замедления. - Выражение через время нам неудобно, поэтому, зная, что время в случае торможения до полной остановки будет t=V/a, мы можем выразить тормозной путь следующим образом:
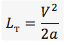
- По II закону Ньютона, ускорение торможения у нас a=Fтр/m, где Fтр — сила трения, а m — масса авто. Подставим это в уравнение и получим:
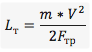
- Вспоминаем формулу силы трения (см. выше):
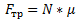
- Получаем формулу тормозного пути, в которой опять сокращается масса:

- Итоговая формула тормозного пути выглядит так (особо подозрительные могут вновь проверить размерность формулы):
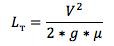
Как ты можешь видеть в результате, тормозной путь вновь не зависит от массы авто m.
В данном случае оговорки по распределению масс и коэффициенту μ ровно те же, что и в предыдущем пункте. Но и здесь можно вполне уверенно подтвердить эти теоретические выкладки практикой. Телеметрия уверенно говорит, что автомобили совершенно разной массы на одинаковой модели резины тормозят практически одинаково.
Резюме
Вывод достаточно простой. Если масса автомобиля особо не влияет на торможение и прохождение поворотов, на что же она влияет? Естественно, на разгон. Тут уж масса никоим образом сократиться из уравнения не может. Именно поэтому я и говорил, что основной глобальной характеристикой автомобиля является тяговооруженность. Именно по ней обычно и разбиваются автомобили по классам в регламентах соревнований.
Вместо Post Scriptum
На что еще влияет масса, а точнее распределение масс частей автомобиля относительно вертикальной и продольной оси, так это момент инерции. Не буду углубляться в суть этого понятия, но он влияет на т.н. «вертлявость» автомобиля, т.е. способность автомобиля к быстрому изменению пространственного положения, а точнее легкость начала вращения относительно оси. Однако низкий момент инерции, или высокая вертлявость, если хочешь, не даст серьезного преимущества на треке (как и низкий момент инерции маховика двигателя не делает двигатель мощнее). Но надо понимать, что более тяжелые автомобили, как правило, обладают большим моментом инерции.
